【小学3年生の壁】あまりある割り算の問題解説と解き方のポイント、考え方について
「割り算」は小学生の算数の中でもつまずきやすい単元の一つです。
特に「あまりのある割り算」は、概念を理解するのが難しくきちんと理解できていないまま授業での学習を終えてしまう子どもが多くいます。学校の宿題に取り組んでいても思うように進められず、保護者が質問を受けることも多いのではないでしょうか。しかし、教えようと思っても「計算したらこうなるでしょ」という説明だけでは理解してもらいにくいのがあまりのある割り算の難しいところです。
この記事では、小学3年生の壁とも言われている「あまりのある割り算」を子どもに教えるために必要な考え方や解き方のポイントを紹介します。例題も交えて解説していくので、子どもにわかりやすく教えるためのヒントにしてください。
小学3年生の壁「あまりある割り算」について
小学校3年生になると、それまでに学んできた足し算・引き算・掛け算に加えて新たに学ぶのが割り算です。小学校2年生までは算数が得意でも、小学校3年生で割り算が入るとつまずいてしまい、算数への苦手意識を持つきっかけになることも多くあります。
特に「あまりのある割り算」は、親がいざ子どもに教えようと思っても意外と説明するのが難しい単元として有名です。ここからは「あまりのある割り算」の考え方について紹介していきます。子どもが算数嫌いにならないよう、丁寧に教えるためのヒントにしてみてください。
あまりとは何か?
「あまり」とは、20÷3の計算のようにきれいに割り切れないときに出るあまった数のことです。言葉だけで伝えるのは難しいので、子どもに教える時は実際に実物を見せながら教えるのが良いでしょう。
例えば、20÷3を計算するのであれば、家にあるお菓子などを使って20粒手元に用意して、3人に平等な数になるように配ってみましょう。1粒ずつ配っていくと、一人あたり6粒配り終えたところで2粒手元に残ります。平等に配らなければならないので、この手元に残った2粒が「あまり」です。
改めて式にすると、20粒を3人で平等になるように割ったら一人6粒ずつとあまりが2粒になるので
「20÷3=6あまり2」となります。
また、「あまりの数は割る数よりも小さくなる」ということをポイントとして教えるのが大切です。
例えば20粒を3人に5粒ずつ分けるとあまりは5粒になりますが、割る数3に対してあまりが5というのは割り算として成立しません。式にすると「20÷3=5あまり5」となり、割る数の「3」よりもあまりの数「5」の方が大きくなるので割り算としてはNGです。
実際にもう一周1粒ずつ配って見せればまだ配れることがわかるので、なぜNGなのかが子どもにも伝わりやすくなります。割り算を考えるときのルールとして子どもにしっかり伝えておきましょう。
同じようにお菓子を使って配る人数を変えたり、量を変えて練習してみることで理解が深まります。算数の式にするところまでを一緒に練習することで、式の意味を正しく理解できるようになるので根気強く繰り返し取り組みましょう。
・実物を見せながら教える。
・あまりの数は割る数よりも小さくなる。
・根気強く繰り返し取り組む。
「あまりある割り算」の問題の種類
「あまりのある割り算」には問題のパターンがあります。それぞれ例題を通して触れておくことで、より理解を深めていきましょう。実際に「天神」に収録されている問題を見て、解きながら考えてみましょう。
1人分の個数を求める問題
割り算の問題で最も多く問われるのが「1人分の個数を求める問題」です。この問題のタイプの問題の答えは、計算式を答えたり、「1人分は〇個になって、□個あまる」などの答えになります。
( )にあてはまる数を答えなさい。
みかんが18こあります。
8こずつふくろにいれると( あ )ふくろできて、( い )こあまります。
答え:あ(2) い(2)
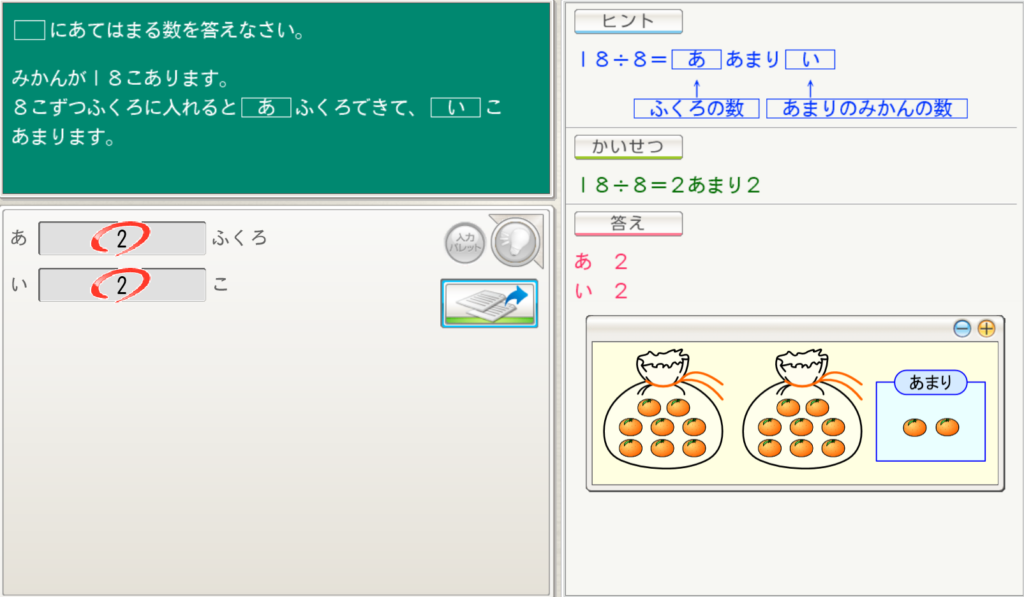
例題は穴埋め問題ですが、文章題に取り組むときは「式にする」ことと、答えを「文章で答える」ことを習慣づけるようにしましょう。
ちなみに、式の答え方には「18÷8=2あまり2」と「18÷8=2…2」の2種類があります。
どちらも表している意味は同じですが、学校の授業によって指示する書き方が違うので子どもの混乱を招かないようにできるだけ学校の指示に合わせて教えましょう。
自宅でも学校で解くときと同じ解き方をすることで、授業を通してさらに知識を定着させられます。
計算が割り切れるかどうかの問題
式を計算した時に答えが割り切れる数字になるかどうかを問う問題です。具体的には以下の例題のような問われ方があります。
つぎの①~③の計算を、ア「わり切れる」、い「わり切れない」のどちらかに分けたいと思います。ア、イそれぞれに当てはまる式を、①~③からすべて選びなさい
①36÷7
②48÷6
③25÷5
答え:ア②,③ イ①
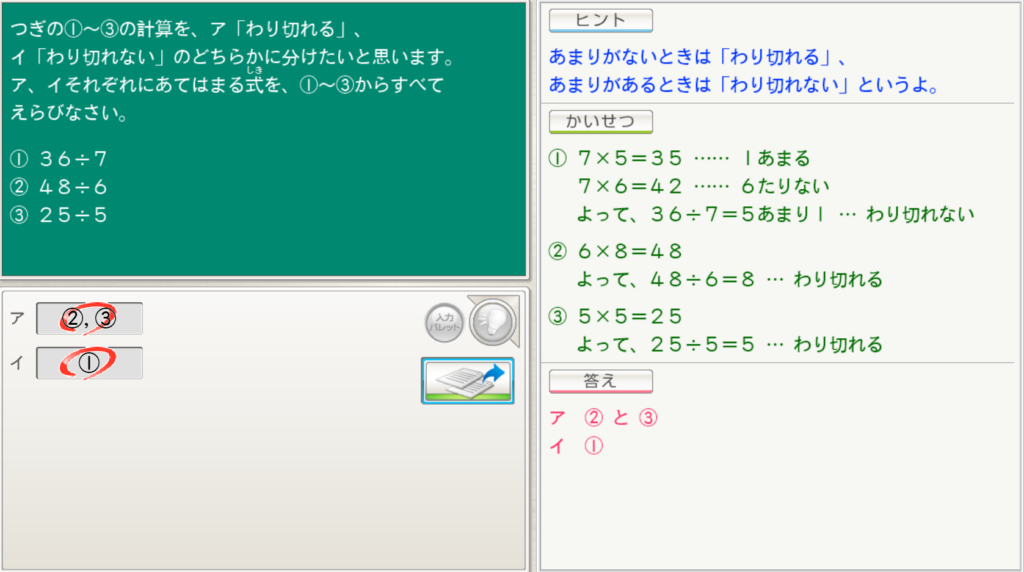
それぞれの解き方を見ていきましょう。
割る数が1桁の数字の場合、割る数の九九の段を使って割られる数を出せるかどうかを考えていくのが効率的です。
例えば、「①36÷7」は36になる7の段を考えていきますが、36という答えになる7の段の九九はありません。
「7×5=35」もしくは「7×6=42」が近い数字になります、どちらもきれいに36にはならないので①は「割り切れない」が答えです。
「②48÷6」であれば6の段で48が出せるかどうかを考えます。
「5×8=48」であまりは出ないので、②の答えは「割り切れる」です。
同じように「③25÷5」も25の答えになる5の段を考えると「5×5=25」になり、あまりが0になるので「割り切れる」となります。
このように九九をベースにして考えていくとスムーズに答えを導くことができます。
計算が正しい方を選ぶ問題
すでに式を計算して答えまで書かれており、その計算が正しいかどうかを問うというタイプの問題があります。実際に例題を紹介しながら解説していきますので、確認していきましょう。
つぎの計算で正しい方をえらびなさい
①79÷9₌8あまり7
②79÷9₌7あまり16
答え:①
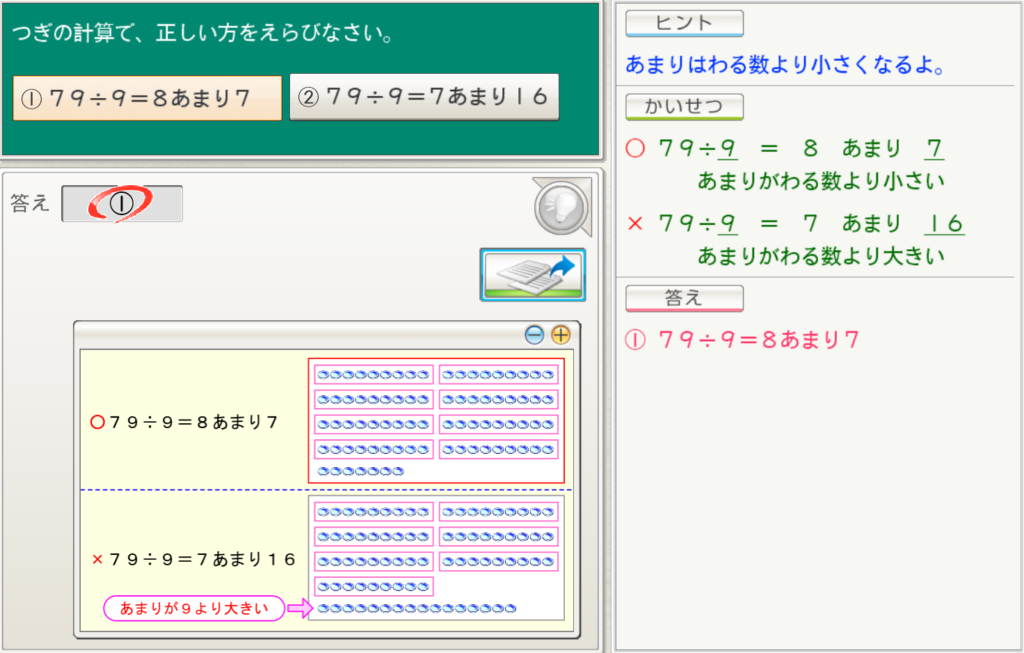
このパターンの問題では、確かめ算を通して確認していくことで、スピーディに答えに辿り着くことができます。
「答え×割る数+あまり」を計算して割られる数と同じになれば「正しい」、同じでなければ「間違い」です。
①「79÷9₌8あまり7」で「8(答え)×9(割る数)+7(あまり)」で79(割られる数)になるかどうかを確かめてみましょう。
「8×9+7=79」となるので、①は「正しい」と言えます。
②「79÷9₌7あまり16」も同じように確認していきます。
「7(答え)×9(割る数)+16(あまり)=79」になるので、こちらも「正しい」が答えですが、こちらの式は「あまり」が「割る数」より大きいので間違いとなります。
全体の数(割られる数)に他の数字を逆から計算して戻せるかどうかをチェックすれば良いのですが、子どもに教えるときは「解き方」ではなく「なぜこうしたら確かめられるのか」を理解してもらうことが大切です。
例題をいくつも使いながら、実物を使って説明して理解を深めていくと良いでしょう。
正しい答えを導く問題
誤った計算から正しい答えを導くという問題のパターンがあります。こちらの問題も例題を用意していますので、確認してみましょう。
つぎの計算はまちがっています。
正しい答えになるように、( )にあてはまる数を答えなさい。
37÷6=5あまり7 ⇒ ( あ )あまり( い )
答え:あ( 6 ) い( 1 )
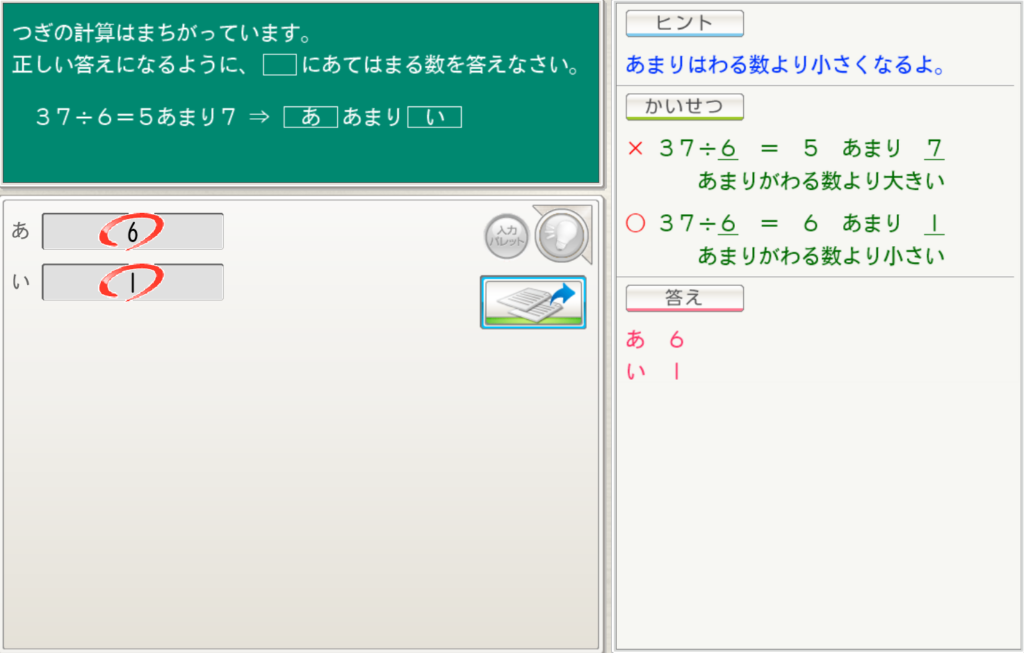
答えは「6あまり1」となっていますが、なぜこの答えが間違っているのかから考えていく必要があります。「あまりとは何か?」でも解説しているように、割り算ではあまりの数は割る数よりも小さくなければいけません。
今回は割る数「6」よりもあまり「7」の方が大きい数字になっているので、「7」という数の中に「6」が含まれていることになります。(「〇〇〇〇」←この4のかたまりの中には3「〇〇〇」が含まれていますね!)
つまり37÷6=5あまり7ではまだ割れることになるので十分ではなく、37÷6=6あまり1が割れる数の最大の数になるのです。
ちなみに37÷6=7になると、割られる数の37では数が足りないので7以上ではないことがわかります。
そのため、答えは「(6)あまり(1)」です。
言葉だけで子どもに説明して理解してもらうのは難しいので、なぜ間違っているのかから一緒に考えて答えを検証していくようにしましょう。
掛け算の変換問題
最後に紹介するパターンは割り算を掛け算に変換して答える問題です。この問題を解くには、そもそも割り算の答えを確かめるためには掛け算が必要だということを理解してもらう必要があります。「こういうものだから」と教えてしまうのは簡単ですが、「なぜ」を知ってもらうことで算数の根本的な部分を理解しやすくなります。
61÷7の計算について、答えをたしかめるには、( )にどんな数を入れるとよいですか。
7×( あ )+( い )=61
答え:あ( 8 ) い( 5 )
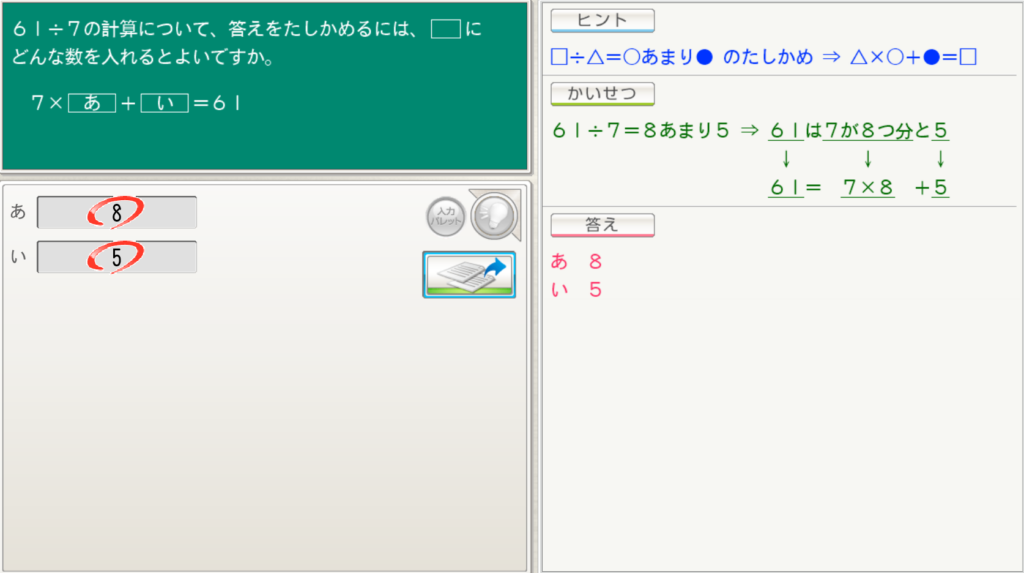
61÷5の計算について答えを確かめる場合( )にどんな数を入れるとよいでしょう
7×( )+( )=61
まずは、「7」を掛けて「61」より小さく最も近い答えになる数字が何かを考えます。
何を掛けてもちょうどの数にはなりませんが、近い数になるのは7×8もしくは7×9です。
しかし、7×9=63となり、「61」よりも大きな数字になってしまいます。
後ほど「+( )」の計算が待っていることを考えると、63では何を足しても「61」にすることはできないので適していません。
そのため最初の( )は「61」よりも小さく最も近い数になる「8」を入れるのが正解です。
続いて2つ目の( )の中を考えていきましょう。
ここまでで「7×8」までは求められたのでこの時点で「56」という数が出ていることになります。
「=61」にするためには「56」に何を足せばよいのかを考えていきましょう。
56+5で「61」になるので、2つ目の( )の答えは「5」です。
わかってしまえば持っている知識で十分に対応できる問題ですが、解き方に慣れるまでしっかり練習しておくことが大切です。
「あまりのある割り算」の考え方
「あまりのある割り算」の考え方を理解するためにおすすめの方法を紹介します。すぐにできることばかりですので、ぜひ取り入れてみてください。
絵や図を使って考える
子どもにあまりのある割り算を教えるときは、絵や図などを使って目で見ながら学べるように工夫しましょう。考える過程をできるだけ視覚化して伝えることで、理解が深まります。
「こうやって解けば良い」と教えた方が一時的な理解は早いのですが、それでは割り算の概念を理解することができず算数としての応用力は身につきません。概念の理解を促すのは時間がかかりますが、子どもの力を伸ばすためにも根気よく丁寧に伝えていくことが重要です。
おはじきやメダルなどを使って考える
実際に動かすことのできるおはじきやメダルなどを使って考えると、割り算が表していることが各段にイメージしやすくなります。簡単な文章題などを使いながら、子どもに手を動かしながら考えさせてみましょう。絵や図を使って教えられたことを、自分の頭の中で整理して理解を深めることができます。
ポイントは、保護者はできるだけ見守る姿勢を貫くということです。答えを伝えたり、軌道修正することなく、子どもが自力で答えに辿り着けるまでじっくり見守ってあげてください。自分でやり遂げたという達成感が自信になり、算数へのやる気に繋がります。
割られる数を順に並べて整理する
割られる数を同じ割る数の式で順番に並べてみるのも、あまりのある割り算の考え方を正しく理解するためには効果的です。
具体的には以下のようなイメージです。
9÷3=3
10÷3=3 あまり1
11÷3=3 あまり2
12÷3=4
13÷3=4 あまり1
14÷3=4 あまり2
15÷3=5
16÷3=5 あまり1
このように並べてみることで、あまりの数は必ず割る数よりも小さい数字になるということを改めて確認できます。実際に目で見てみることで納得感が高まり、理解が深まるでしょう。
九九表を確認しながら取り組む
あまりのある割り算に取り組むときは、九九表を手元に置いて取り組むのがおすすめです。
例題で解説してきたように、割り算の計算では九九をベースにして考えることが多いのでぜひ用意しておきましょう。割られる数に近い数にするには・・・と考えるときに九九表があると数を見比べながら考えやすくなります。九九表を手元に置いていると「九九表がないと解けない状態にならないか不安」という保護者の方もいるかもしれません。しかし、九九表を見ながら取り組むことで割り算に集中できるので考え方を定着させやすくなります。
演習を繰り返しているうちに九九表がなくてもすらすらと取り組めるようになるので問題ありません。まずはあまりのある割り算の考え方の習得に専念できるように、環境を整えていきましょう。
反復学習を行う
あまりのある割り算の解き方を習得するには、とにかく反復学習することが重要です。
子どもが理解しやすいように例題などを使って教え、その場では「わかった!」「できた!」と嬉しい表情を見せてくれるかもしれません。しかし、一度や二度解けただけでは定着は難しく、学校で再度取り組むときにはわからなくなってしまうこともあります。
数日をかけて何度も練習することが大切です。繰り返し学習していくことで、解くスピードも正答率も上がり知識を定着させることができます。
子どもがあまりのある割り算を得意な単元にできるように、しばらくの間は反復学習に取り組むようにしましょう。
まとめ
小学校3年生で学習する「あまりのある割り算」は子どもにとって特につまずきやすい単元の一つです。学校の授業でわからなくなってしまうことも多くある単元ですが、自宅でしっかりサポートして理解を促すことで自信を持てるようになります。
お子様が算数を得意科目にできるように、ご家庭でも根本的な理解が深められるように根気強く教えていきましょう。記事の中で紹介したポイントを参考にしながら、ぜひ一緒に取り組んでみてください。
「あまりある割り算」の問題のコツはわかったけれど、実際に取り組むのは大変そう・・・と感じられた方へ
「あまりある割り算」に限らず、小学校3年生からの問題はつまずくことも増えてくるため予習を必ずしておきたいものです。しかし、保護者が常に付き添って分からない問題に気付くのは、家事、育児、仕事などをしながらだとなかなか難しいかもしれません。
解けない問題が無いように、基礎をバランスよく身につけ漏れなくしっかり準備を進めたい、でも忙しい!という方なら、特におすすめです。「天神」では、「あまりある割り算」の問題だけでなく、小学校で学ぶ問題を学年ごとに収録し、保護者様が特別な準備をしなくても、パソコン一つで様々な教科の問題に取り組むことが出来るツールです。
もし「気になる」と思われましたら、お気軽に資料をご請求ください。早く始められるほどコスパよくご利用いただけます。
豊富な類題と問題数でとことん反復練習
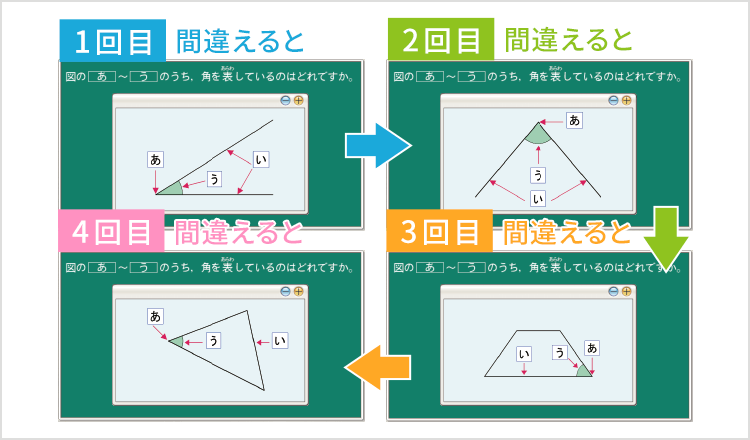
問題文章や選択肢が変わったり、異なる図形が表示されたり、問題数が多く類題も豊富です。あまり理解できていないまま答えを覚えて先に進んでしまうことがありません。テスト学習モードでは範囲を選ぶと、問題がシャッフルして出題されますので、学校でのテストに備えられます。
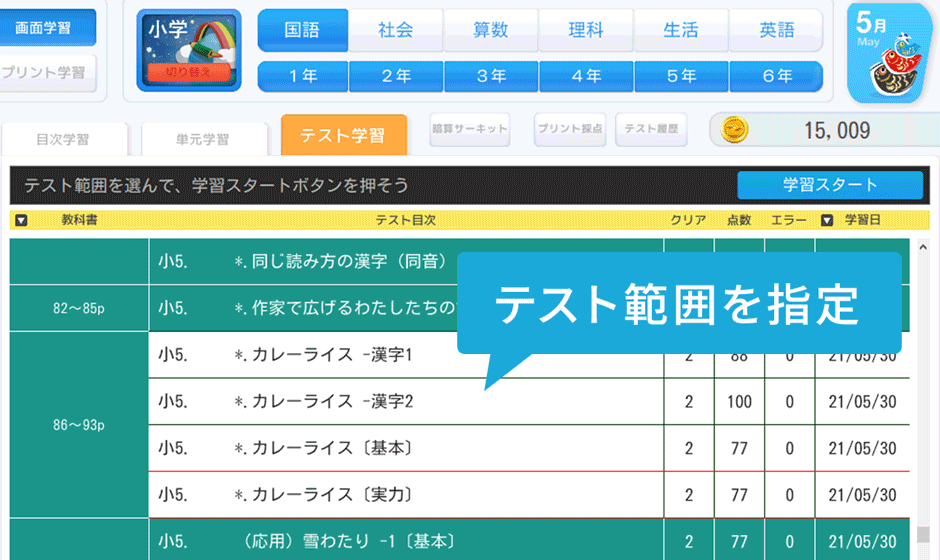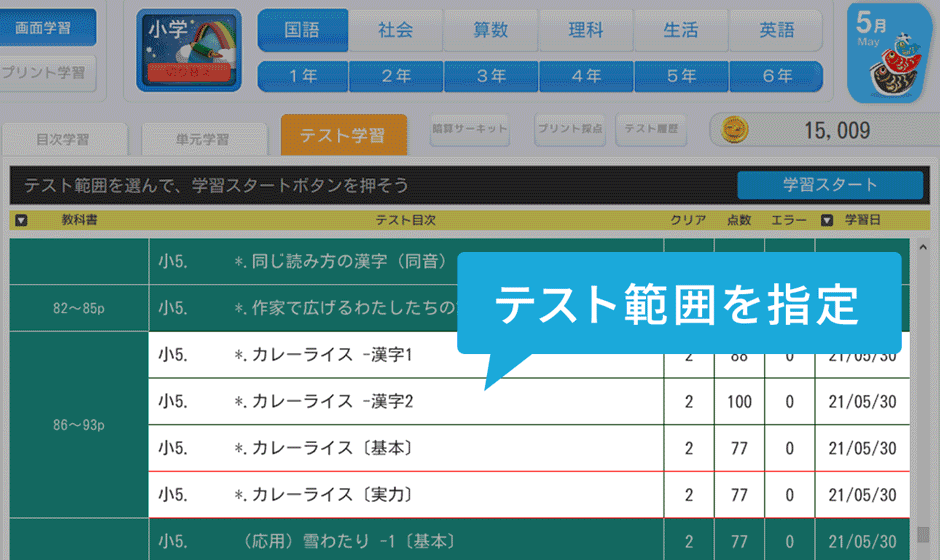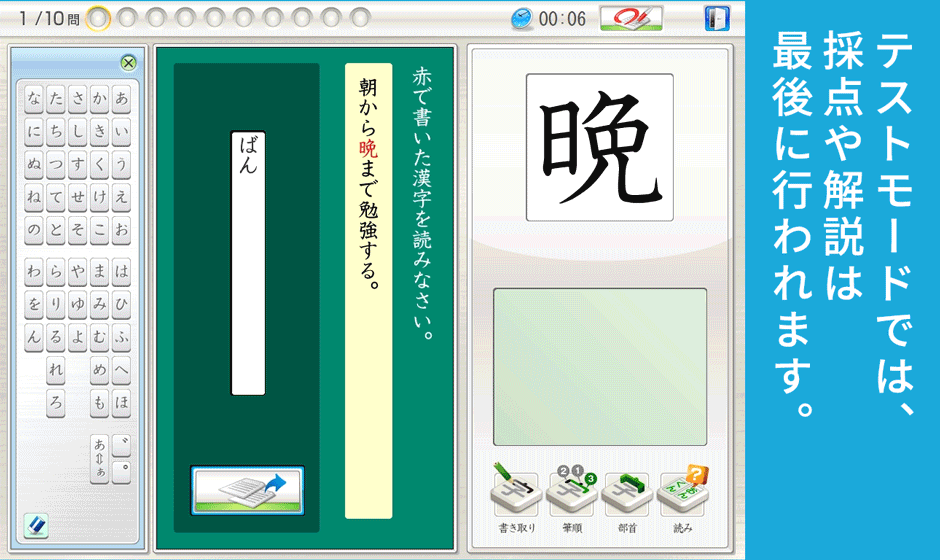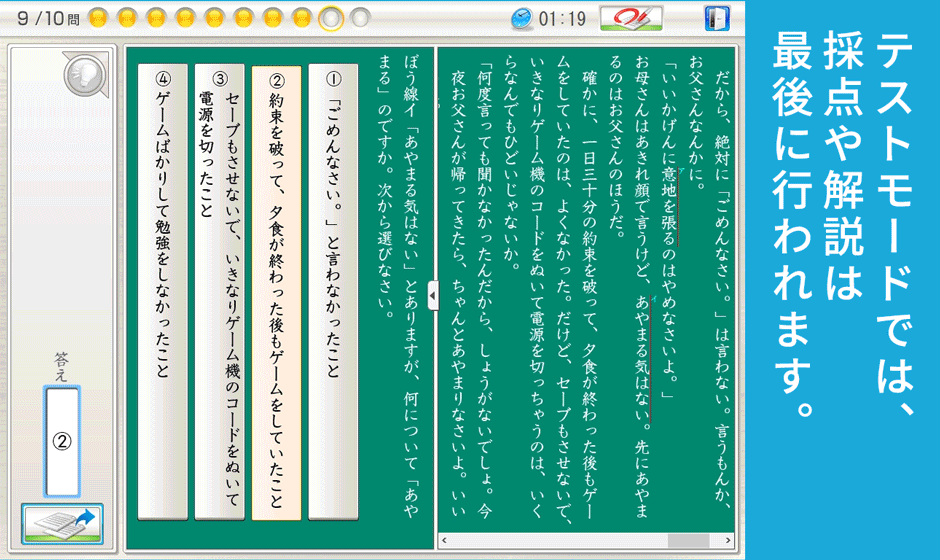
プリント可!「書いて解く」紙教材としても活用OK
画面で学習していたときには選択問題形式だったものが、プリントで学習するときには穴埋め問題形式に変わるものも。画面とプリントの成績を別々に記録するので豊富な問題数による反復学習と、画面とプリント学習でたしかな学力を身につけます。
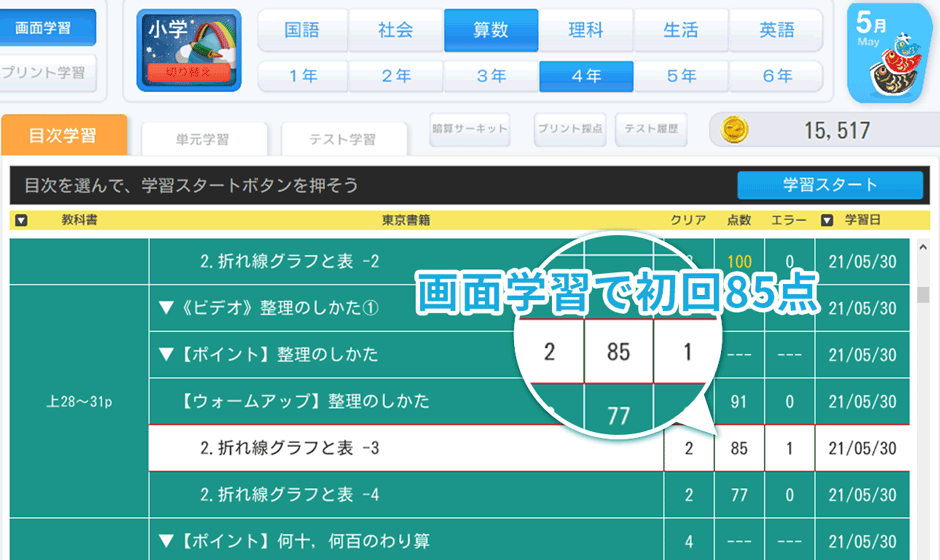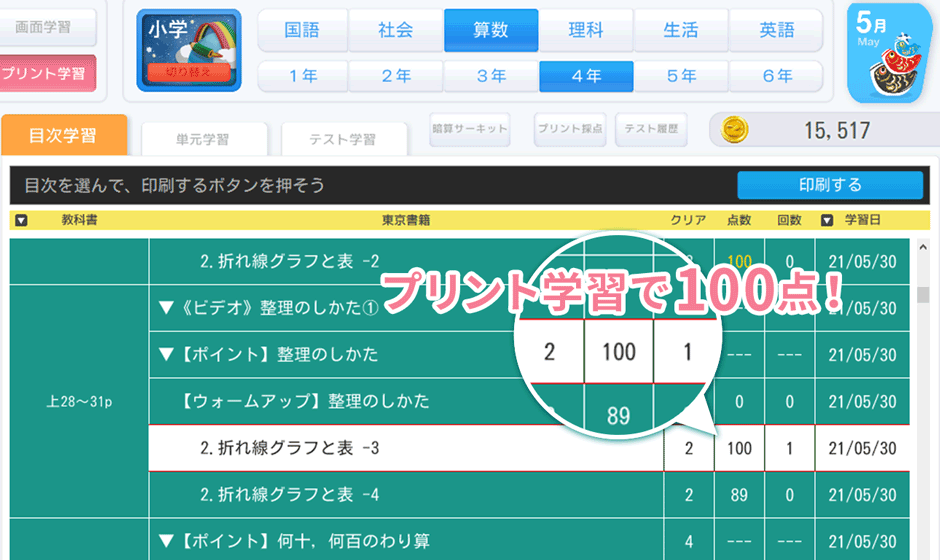
現在、「天神」では無料体験を実施しています。
学校の授業についていけなくなる前に、基礎をバランスよく身につけたい。
中学入試本番に向けて、漏れなくしっかり準備を進めたい。
と考える親御さまは、下記バナーから、ぜひ無料の資料請求と体験申込をしてみてください。


